1. 研究的理论基础 1.1 多元智能理论 基于对传统智商概念和智能一元化的怀疑,美国发展心理学家霍华德加德纳于1983年提出了多元智能理论。他将智能定义为:“在特定的文化背景下或社会中,解决问题或制造文化产品的能力。”他认为智能是多元的(音乐智能、身体运动智能、数学逻辑智能、语言智能、空间智能、人际关系智能、自我认识智能等),而智能的选择既源于生物学,又要考虑根据一个或多个文化背景来评价。加德纳提出,每个正常人都在一定程度上拥有多项智能,人类个体的不同在于所拥有的智能的程度和组合不同。因此,在教学中若注意鉴别并发展学生的优势智能,并帮助学生将优势智能的特点迁移到其他智能领域,则有利于最大限度地开发学生的智能。 1.2 建构主义理论 根据皮亚杰的认知建构主义观点,学习不是来自能够转移到人的头脑中的事物信息,而是来自学习者与环境之间的极为重要的建构性的相互作用,其过程在很大程度上受到学习者先前知识的影响。强调学习的过程是一个主动建构的过程,如果信息被用于解决问题,那么它的作用是工具而不是孤立的事实,信息如何呈现是非常重要的。维果斯基的建构主义理论中,文化为孩子们提供了发展的认知工具,这些工具的类型和质量决定了孩子们的发展图式和发展等级。就是说学生的学习成果取决于学生带到课堂中的知识、目的、动机以及他生存的文化和生活背景。建构主义的观点应用到现代课堂教学中,强调学生头脑中已有的知识是他同化新知识的基础,只有当学生已有的知识与新知识之间产生了本质的联系,即教学必须寻找到学生的“最近发展区”,为学生提供适当的情景时,有意义的学习才会发生。由于学生原有的知识水平不同,学习的目的、动机以及生存的文化和生活背景也存在差异,所以实施差异化的教学,帮助学生主动建构自己的科学概念是必要的。 1.3 数学学习力的模型 数学学习力的模型是由数学能力及其各个核心要素之间的构成的一个综合系统。 数学学习力的核心组成要素,包含两部分六要素:数学知识与经验、合作与交流、 数学活动、策略与反思、动机与信念、批判与创新。 数学学习力通过以上模型中的六项核心要素来体现。这些要素是个性化的,又 是相互影响的,共同协作促进学生的数学学习力的发展。该模型参照DeakinsR.Crick 教授双螺旋理论,由两个三角形组成,正三角由策略与反思、动机与信念、批判与 创新组成,代表了学习个体的学习意愿,形成批判创新的思想是其发展的最高形式; 倒三角由数学知识与经验、合作与交流、数学活动组成,代表了学习个体数学能力的 发展,知识与经验是基础,其数学能力的发展是在数学活动、合作与交流中进行的, 正反三角形相互作用促进学习个体的数学学习力。六个要素的具体阐述如下: 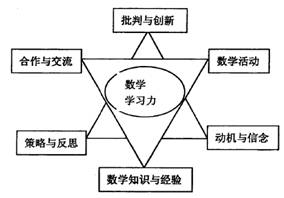
2. 研究的方法 本课题主要采用文献法、问卷调查法、访谈法、统计分析法和行动研究法等研究方法进行研究。 (1)对有关理论依据的研讨及国内外相关经验的研究状况,主要采用文献研究法; (2)调查研究部分主要采用问卷调查法,并辅之以访谈法,获取研究所需的各种资料; (3)论文的撰写部分采用定性研究与定量研究相结合的方法,对问卷结果进行统计分析。 |