三视图

人教B版高一必修二

目录

第一章立体几何初步

第一节构成几何体的基本元素

第二节棱柱、棱锥和棱台的结构特征

第三节圆柱、圆锥、圆台和球

第四节投影与直观图

第五节三视图

第六节棱柱、棱锥、棱台和球的表面积

第七节柱、锥、台和球的体积

第一章立体几何初步

第五节三视图

我的学习目标

（1）了解空间图形的不同表示形式

（2）掌握画三视图的基本技能

（3）能画出简单空间图形（长方体、球、圆柱、圆锥、棱柱等的简易组合）的三视图，能识别这样的三视图所表示的立体模型；

重点：画出简单组合体的三视图

难点：识别三视图所表示的空间几何体

我的学习过程

一.生活引入

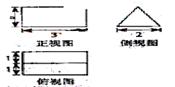
1.观察下图工程图纸说出这个物体是个什么几何体？

2.图中三个平面图形是怎么形成的？

 

二、基本功训练

1、知识点学习

（1）知识点1：掌握三视图的基本技能。

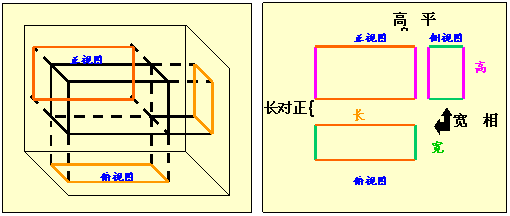
a.三视图的理论依据是正投影

b.形成三视图的三个面的特征及布局

c.在三个面中几何体的投影分别是什么

球的三视图都是         ；长方体的三视图都是           ；圆柱的主视图、左视图都是          ，俯视图是           ；圆锥的主视图、左视图都是              ，俯视图是          。

简易分析：此题实际上属于三视图画法问题

（2）知识点2：能画出简单空间图形（长方体、球、圆柱、圆锥、棱柱等的简易组合）的三视图，能识别这样的三视图所表示的立体模型

下列几何体各自的三视图中，有且仅有两个视图相同的是（    ）

 

 

A．①②        B．①③       C．①④       D．②④

简易分析：此题考查简单几何体的三视图。

2 、知识点演练

（1）变式演练1：小明从正面观察如图所示的两个物体，看到的是（    ）

 

 

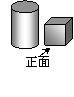
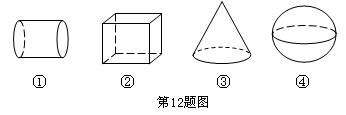
（2）变式演练2：如图，下列四个几何体中，它们各自的三视图（主视图、左视图、俯视图）有两个相同，而另一个不同的几何体是_______.（把所有符合条件的都写上）

 

 

 

三、题型训练

1、选择题(10分)

（1）如果用□表示一个正方体，用   表示两个正方体叠加，用█表示三个正方体叠加，那么图中由6个正方体叠成的几何体的主视图是 ( B    )

 

 

 

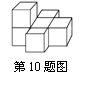
（2）一个四棱柱的俯视图如右图所示，则这个四棱柱的

主视图和左视图可能是（D   ）

 

2、填空题(8分)

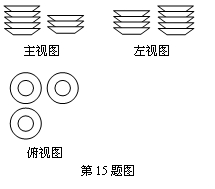(1)一张桌子上摆放若干碟子，从三个方向上看，三种视图如图所示，则这张桌子上共有碟子    12  个.

 

 

 

 

 

(2)用小正方体搭成一个几何体，下图为它的主视图和左视图，搭成这个几何体的小正方体的个数最多为        个。

                   主视图        左视图

3、解答题 (24分)

（1）画出它的直观图   

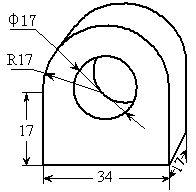
(2)如图是一个零件的直观图（单位mm），画出这个几何体的三视图

 

四、学以致用

1、 我要解决生活中实际问题。(6分)

 

2、每课一测(10分)

(1)如图所示是由一些相同的小正方体构成的几何体的三视图，则组成

这个几何体的小正方体的个数是（    ）

A.4          B.5          C.6         D.7

 

 

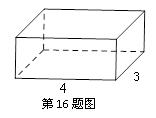(2)如图所示，水平放置的长方体的底面是边长为3和4的矩形，它的左视图的面积为6，则长方体的体积等于        .

 

 

[来源:学§科§

(3)已知一个正三棱柱的底面边长为3cm,高为5cm,画出这个正三棱锥的三视图