导数的概念
湖南教育出版社
目录
第二章 导数与微分
第一节 导数的概念
第二节 函数的求导法则
第二章 导数与微分
第一节 导数的概念
第一课时
我的学习目标:
1、学习导数概念的实际背景.能描述导数的概念掌握表达形式,会用导数(变化率)描述简单的实际问题;
2、会利用导数的定义来求一些简单函数的导数及几个基本初等函数的导数公式
3、了解导数的几何意义,会用导数求曲线的切线和法线方程;
4、了解可导与连续的关系
我的学习过程
一、生活引入
1、物体做变速直线运动的平均速度![]() ;函数的极限
;函数的极限![]() 。(5分)
。(5分)
2、物体在做变速运动时,如何求这个物体在![]() 时刻的瞬时速度? (5分)
时刻的瞬时速度? (5分)
例如:在高台跳水运动中,运动员相对水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系![]() ,计算运动员在
,计算运动员在![]() 这段时间里的平均速度,并思考下面的问题:
这段时间里的平均速度,并思考下面的问题:
(1)运动员在这段时间里是静止的吗?
(2)你认为用平均速度描述运动员的运动状态有什么问题吗?
二、基本功训练
1、知识点学习
(1) 知识点1:认识平均变化率及瞬时变化率:(5分)
![]() 从
从![]() 到
到![]() 的平均变化率是____________;y=f(x)在
的平均变化率是____________;y=f(x)在![]() 处的瞬时变化率是____________
处的瞬时变化率是____________
简易分析:此题实际上属于(逼近思想 )问题
(2) 知识点2:学习导数的定义 (5分)
![]() 在
在![]() 处的导数记作 ,即______________。把上式中的
处的导数记作 ,即______________。把上式中的![]() 看作变量x时,
看作变量x时,![]() 即为f(x)导函数,简称导数,即
即为f(x)导函数,简称导数,即![]() = 。
= 。
简易分析:探索新知识
(3)知识点3:了解导数的几何意义 (8分)
导数的几何意义是什么?函数的可导性与连续性有什么联系?
简易分析:斜率问题
2、知识点演练
(1)变式演练1:利用求导公式![]() ,求函数
,求函数![]() 的导数。(10分)
的导数。(10分)
(2)变式演练2: (15分)
已知一个物体运动的位移S(m)与时间t(s)满足关系S(t)=-2t2+5t,求:
1求物体第5秒和第6秒的瞬时速度
2求物体在t时刻的瞬时速度
三、题型训练
1、选择题(5分)
(1)下面说法正确的是( )
(A)若曲线![]() 在点
在点![]() 处没有切线,则
处没有切线,则![]() 有可能存在
有可能存在
(B)若![]() 不存在,则曲线
不存在,则曲线![]() 在点
在点![]() 处没有切线
处没有切线
(C)若曲线![]() 在点
在点![]() 处有切线,则
处有切线,则![]() 必存在
必存在
(D)若![]() 不存在,则曲线
不存在,则曲线![]() 在点
在点![]() 处切线斜率不存在
处切线斜率不存在
2、填空题 (12分)
(1)已直函数![]() ,当
,当![]() 时,
时,![]()
(2)![]() = ;
= ;![]() = ;
= ;![]() = ;
= ;![]() = ,
= ,
(3)用导数来表示曲线![]() 在点
在点![]() 处的切线斜率k= 。
处的切线斜率k= 。
3、计算题(10分)
求曲线![]() 在点(2,8)出的切线方程和法线方程。
在点(2,8)出的切线方程和法线方程。
四、学以致用
1、 我要解决生活中实际问题。(10分)
当物体的温度高于周围介质的温度时,物体就不断的冷却。设物体的温度t与时间t的函数关系为T=T(t),则![]() 成为物体在时间
成为物体在时间![]() 内的平均冷却速度,求物体在t时刻的冷却速度是?
内的平均冷却速度,求物体在t时刻的冷却速度是?
2、每课一测(10分)
对于均匀细棒,单位长度的细棒的质量成为这细棒的线密度。一根质量非均匀分布的细棒放在x轴上,在[0,x]上的质量m是x的函数m=m(x),应怎样确定细棒上点![]() 处的线密度?
处的线密度?
附:答案和解析
一, 答,(1)不是 。 (.虽然平均速度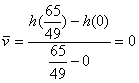 ,但我们知道运动员在这段时间内并没有“静止”。)
,但我们知道运动员在这段时间内并没有“静止”。)
(2)平均速度不能,而瞬时速度才可以描述运动员的状态。
二,1、(1)![]() ;
;![]() ;
;
(2)![]() ;
;![]() ;
;![]() .
.
(3)几何意义:函数![]() 在点
在点![]() 处的导数
处的导数![]() 在几何意义上表示曲线
在几何意义上表示曲线![]() 在点
在点![]() 处的切线斜率。
处的切线斜率。
函数的连续性和可导性的关系:连续不一定可导,但可导一定连续
2、(1)![]()
(解析:![]() )
)
(2)1![]() ;
; ![]() ; 2
; 2![]()
(解:1![]()
![]() ;
; ![]()
因此第5秒的瞬时速度![]() ,同理可得
,同理可得![]()
2把上式中的5看成t得![]() )
)
三、1、选择题
D
( 如果你选A,说明你已经懂得了导数和切线斜率之间是存在关系,但是搞不清楚切线、切线斜率以及![]() 之间的存在关系。
之间的存在关系。
如果你选B,说明是你已经掌握了导数和切线斜率之间的一般关系,只是忽略了特殊情况:当![]() 时,切线是垂直于x轴的直线
时,切线是垂直于x轴的直线![]()
如果你选C,可以看出你已经理解了导数的几何意义,只是忽略了当![]() 时,有切线,但
时,有切线,但![]() 是不存在的.
是不存在的.
因为当![]() 时,
时,![]() 是不存在的,虽然有切线,但切线斜率是不存在的.
是不存在的,虽然有切线,但切线斜率是不存在的.
,所以正确答案是D。)
2、填空题
(1)3;(解:![]() )
)
(2)0;![]() ;
;![]()
![]()
(3)![]()
四、1、![]()
2、![]()
第二课时
第二章 导数与微分
第二节 函数的求导法则
我的学习目标:
- 掌握导数的四则运算法则
- 学会运用基本初等函数的导数公式及导数的运算法则来求比较复杂函数的导数.
- 导数的一些应用.
我的学习过程
一、生活引入
1、![]() = (C是常数);
= (C是常数);![]() = ;
= ;![]() ;
;![]() ;
;![]() = ;
= ;![]() = 。 (6分)
= 。 (6分)
2、上一节课我们学习了利用导数的定义来求一些简单函数的导数,且求出了几个基本初等函数的导数公式,但对于求较复杂的函数是比较困难的,例如:函数![]() ,
,![]() ,
,![]() 等这些函数的导数怎么求? (6分)
等这些函数的导数怎么求? (6分)
二、基本功训练
1、知识点学习
(1)知识点1:导数的加减法则 ( 5分)
设函数![]() 早点x处可导,则他们的和、差在点x处也可导,且1 。
早点x处可导,则他们的和、差在点x处也可导,且1 。
简易分析:此题实际上属于(加减法运算 )问题
(2) 知识点2:导数乘法法则(5 分)
设函数![]() 早点x处可导,则他们的积在点x处也可导,且2 。
早点x处可导,则他们的积在点x处也可导,且2 。
简易分析:乘法运算
(3) 知识点3:导数商法则(5 分)
设函数![]() 早点x处可导,则他们的商(分母不为零)在点x处也可导,且2 。
早点x处可导,则他们的商(分母不为零)在点x处也可导,且2 。
简易分析:商的运算
2、知识点演练
(1) 变式演练1:(10分)
求![]() 的导数
的导数
(2)变式演练2:(13分)
设![]() ,若
,若![]() ,则
,则![]() 的值是多少?
的值是多少?
三、题型训练
1、选择题(5分)
任一作直线运动的物体,其位移s与时间t的关系是![]() ,则物体的初速度是( )
,则物体的初速度是( )
A. 0 B.![]() C.-2 D.3
C.-2 D.3
2、填空题 (12分)
(1)![]() = ;
= ;![]() = ;
= ;![]() = ;
= ;![]() = 。
= 。
(2)有一质点沿直线运动,从始点起到t时刻的距离![]() ,则质点是在t= 时刻的瞬时速度为零。
,则质点是在t= 时刻的瞬时速度为零。
(3)设曲线![]() 上点x处的切线与直线
上点x处的切线与直线![]() 平行,则点x的横坐标是 。
平行,则点x的横坐标是 。
3、计算题(13分)
求函数![]() 的导数。
的导数。
四、学以致用
1、 我要解决生活中实际问题。(10分)
已知某企业每月生产![]() t产品的总成本为C千元,,C=
t产品的总成本为C千元,,C=![]() ,如果每吨产品的销售价格为2万元,求利润函数
,如果每吨产品的销售价格为2万元,求利润函数![]() 及其导数
及其导数![]() ,以及
,以及![]() ,
,![]() ,
,![]() ,并对结果进行说明。
,并对结果进行说明。
2、每课一测(10分)
设![]() ,求
,求![]() 。
。
附:答案和解析
一, 1、0;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() 。
。
2、可以利用函数的性质把这些函数进行转化,如:函数![]() 可以转化成
可以转化成![]() ,
,![]() 的导数已知,但需要借助四则运算法则才能求出来。
的导数已知,但需要借助四则运算法则才能求出来。
二,1、(1)、![]()
(2)、![]() 特别地,
特别地,![]() (C为常数)
(C为常数)
(3)、![]() 特别地,
特别地,![]()
((1)和(2)可推广到有限个可导函数的运算)
2、(1)![]()
(解:![]() )(2)
)(2)![]()
(解:因为![]() ;则
;则![]()
若![]() ,即
,即![]() ,因此
,因此![]() )
)
三、1、选择题
(1) D
( 如果你选A,说明你已经懂得了自由落体运动的初速度为零,只是本题并不是自由落体运动
如果你选B,说明是你已经掌握了速度等于路程对时间t的导数,只是没有把t=0带入求解
如果你选C,可以看出你会求加速度,只是把加速度看成处速度了
因为![]() ,因此
,因此![]() 。所以正确答案是D。)
。所以正确答案是D。)
2、填空题
(1)![]() ;
;![]() ;
;![]() ;
;![]()
(2)0,1,4 。 (![]() ,当速度为零时,即
,当速度为零时,即![]() ,则
,则![]() 得t=0,1,4 。)
得t=0,1,4 。)
(3)![]() 。(
。(![]() ,有已知条件得
,有已知条件得![]() =6,所以有
=6,所以有![]() ,求得
,求得![]() )
)
3、![]() ;
;
(解:![]() )
)
四、1、![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]()
结果说明:当月产量为8 t时,再生产1 t,利润将增加1.4万元;当月产量为15 t时,再生产1 t,利润将不会增加;当月产量为20 t时,再生产1 t,利润将减少1万元;也就是说,该企业不能单靠增加产量来提高利润。
(解:利润=收入-成本,所以利润函数![]()
从而![]()
![]() (千元/t)
(千元/t)
![]() (千元/t)
(千元/t)
![]() (千元/t))
(千元/t))
2、![]() ;
;![]() ;
;![]()
(解: ![]()
![]()
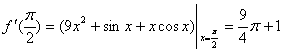 )
)
| 感动 | 同情 | 无聊 | 愤怒 | 搞笑 | 难过 | 高兴 | 路过 |
相关文章
-
没有相关内容


 会员登录
会员登录