人教B版选修2-2演绎推理创意法教育课题申报教案

人教B版选修2-2

第二章 推理与证明

第一节合情推理与演绎推理

              第二章 推理与证明

第一节 合情推理与演绎推理

第二课时（演绎推理）

 

我的学习目标：

1、              知识与技能：

（1）了解演绎推理的含义，了解演绎推理三种不同的推理规则  

（2）能够用演绎推理三种不同的规则进行简单的推理

2、              过程与方法：

（1）通过对实例的分析、归纳总结的过程，培养自己的理性思                           维能力. 

（2）通过实例演练，体会演绎推理的推理思想，培养良好的分析问题、解决问题的能力.

3、情感态度价值观：

通过本节课的学习，感受体会演绎推理三种推理思想，感受演绎推理在数学及日常生活中的应用，培养自己举一反三、以一知十、勇于探索、敢于创新的精神.

我的学习过程：

一、生活引入

1、观察                              

1+3=4=,

1+3+5=9=,

1+3+5+7=16=,

1+3+5+7+9=25=   ,

……

由上述具体事实能得到一般结论为：____________________

你推得结论的过程属于什么推理方式：__________________________

并判断结论的正误______________________________?

（设计目的：考察归纳推理）

2、在平面内，若a⊥c，b⊥c，则a//b.

类比地推广到空间，你会得到什么结论：_________________________

___________________________________________________________

你推得结论的过程属于什么推理方式_________________________

并判断结论的正误______________________________________？

（设计目的：考察类比推理）

分析这两个问题，你能否发现合情推理结论可靠性？ ________

（设计目的：让学生通过归纳推理和类比推理的实例，感知合情推理的不可靠性，从而让学生产生疑问，什么推理才具有可靠性？）

3、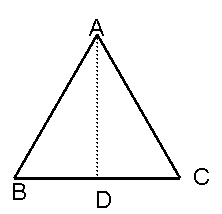判断下面推理是否正确？它是合情推理吗？为什么？

命题：等腰三角形的两底角相等.

已知：如图在中，AB=AC

求证：

证明：作

又因为AB=AC,

AD=AD

所以

因此

体会这种推理方式与合情推理的不同_________________________

（设计目的：该例题每一步的推导都是有一定的公理、定理作为依据，与前两个实例的对比，有很明显的可靠性，从而让学生感知演绎推理的定义）

二、基本功训练

1、知识点学习

（1）、结合情境创设3归纳演绎推理的含义

演绎推理：

（2）、分析下列推理是演绎推理吗？如果是，分析其得出结论的依据？

 

 

所有的金属都能导电,          

因为铜是金属,                    

所以铜能导电 依据为:_______________________________.

 

三角函数都是周期函数

依据为: _______________________.

（3）、你能理解三段论中大前提、小前提、结论的含义吗？

大前提___________________________________.

小前提____________________________________.

结论______________________________________.

（4）、你能用集合语言解释大、小前提、结论吗？

 

 

（5）、你能举一些三段论推理的例子吗？并指出其中的大前提、小前提和结论.

 

（6）、分析下列推理形式是否正确？它们的推理结论正确吗？

 

所有的鹅都吃白菜

      参议员先生也吃白菜

      参议员先生是鹅

 

所有的金属都能导电

碳是金属

所以碳能导电

 

指数函数为增函数

       为指数函数

所以为增函数

 

思考：怎样才保证三段论形式的推理正确呢？

 

知识点演练：

1、三段论推理

例1已知：空间四边形ABCD中，点E、F分别是AB,AD的中点

求证：EF//平面BCD

 

思考1、说出你的推理思路及结论的依据.

     2、你能说出推理的大、小前提吗？

巩固练习：证明函数的奇偶性.

 

 

 

思考：说说你的推理思路，你能指出其中的大前提、小前提和结论吗？

2、传递性推理

自主学习例2，完成下列问题

1、              在整个推理过程中“1”起了什么作用？

 

2、              你能归纳这种推理模式吗？

 

 

3、              完成下列推理

(1) 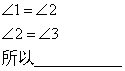                (2)

 

3、完全归纳推理

自学教科书例3完成下例问题

1、          什么是完全归纳推理

 

2、          归纳推理与完全归纳推理的区别

3、          完成下列推理

锐角三角形内角和为180度

钝角三角形内角和为180度

直角三角形内角和为180度

任意三角形包括锐角三角形、钝角三角形、直角三角形

所以___________________________________________________

 

 

 

学以致用：

1、在数列试用合情推理猜想数列的通项公式，用演绎推理来证明.

 

2、每课一测

（1）、分析下列推理是否正确

A、因为正方形的对角线互相平分且相等，所以一个四边形的对角线互相平分且相等，此四边形是正方形.

 

B、已知（m+1)(5m+1)是5的倍数，可知或者m+1是5的倍数，或者5m+1是5的倍数，因为5m+1不是5的倍数，所以m+1是5的倍数.

（2）、下列推理的两个步骤分别遵循哪种推理规则？

 

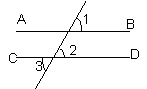因为AB//CD

所以

又因为

所以

答案与解析：

1、解：因为，所以，同理

所以猜想

用演绎推理证明：

所以是以为首相，以为公差的等差数列。

所以=1+

即：

2、(1):   A:错误，因为三段论的推理形式错，四边形不一定是正方形；

         B：正确，考查的是完全归纳的推理规则

（2）第一步用的是三段论的推理，第二步用的是传递性推理。