创意法教育课题申报实施材料:对数函数及其性质
第四课时 对数函数及其性质
我的学习目标:
1、掌握对数函数的概念、图象和性质,在掌握性质的基础上能进行初步的应用。
2、理解反函数的概念,理解对数函数和指数函数互为反函数,能够在同一坐标上看出互为反函数的两个函数的图象性质。
3、掌握对数函数在生产实际中的简单应用。
4、通过对数函数概念的学习,树立相互联系相互转化的观点,通过
对数函数图象和性质的学习,渗透数形结合,分类讨论等思想,注重
观察,分析,归纳等逻辑思维能力的提升。
我的学习过程
一、 生活引入(5分)
当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.根据此规律,人们获得了生物体内碳14含量P与死亡年数t之间的关系式为:![]()
试用![]() 的表达式表示
的表达式表示![]() 。
。
思考t与P的关系,由此引出对数函数的概念。
一般地,当a>0且a≠1时,函数______叫做对数函数,自变量是x; 函数的定义域是(0,+∞)。
二、基本功训练(35分)
1、知识点学习(25分)
(1)知识点1:掌握对数函数的概念(5分)
判断函数![]() ,
,![]() 是否是对数函数。
是否是对数函数。
(2)知识点2:熟练对数型函数定义域的求解(6分)
求下列函数的定义域:
①![]() ;
;
②![]() ;
;
③![]()
(3)知识点3:掌握对数型函数值域的求解(6分)
求函数的值域
①求下列函数的值域
1.![]()
②![]()
③![]()
(4)知识点4:利用对数函数的图象和性质比较函数值的大小。
(6分)
比较大小:
①![]() ____________________________________________
____________________________________________
②![]() ______________________________________
______________________________________
③![]() _______________________________________
_______________________________________
(5)知识点5:了解指数函数和对数函数互为反函数。(2分)
![]() 的反函数是_______;两者的图象关于______对称。
的反函数是_______;两者的图象关于______对称。
2、知识点演练(共10分,每题5分)
(1)变式演练1:比较![]() 的大小。
的大小。
(2)变式演练2:求函数![]() 的定义域。
的定义域。
三、题型训练
1、选择题(共10分,每题5分)
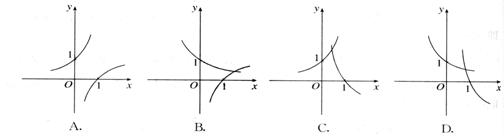
(1)当a>1时,在同一坐标系中,函数![]() 与
与![]() 的图象是( )
的图象是( )
(2)不等式的![]() 解集是( ).
解集是( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2、填空题(10分)
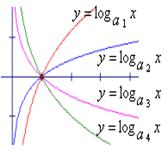 右图是函数
右图是函数![]() ,
,![]()
![]() ,
,
![]() 的图象,则底数之间的关系为 。
的图象,则底数之间的关系为 。
3、解答题(20分,每题10分)
(1)求函数![]() 的定义域。
的定义域。
(2)![]() 的反函数的图象过点
的反函数的图象过点![]() ,求a的值。
,求a的值。
四、学以致用
1、 我要解决生活中实际问题。(10分)
溶液酸碱度的测量问题:溶液酸碱度pH的计算公式![]() ,其中
,其中![]() 表示溶液中氢离子的浓度,单位是摩尔/升。
表示溶液中氢离子的浓度,单位是摩尔/升。
(1)分析溶液酸碱度与溶液中氢离子浓度之间的变化关系?
(2)纯净水![]() 摩尔/升,计算其酸碱度。
摩尔/升,计算其酸碱度。
2、每课一测(10分)
函数![]() 在区间
在区间![]() 上的最大值比最小值大2,求实数
上的最大值比最小值大2,求实数![]() 的值。
的值。
附:答案和解析
一、生活引入
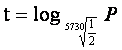 ;
;![]()
二、基本功训练
1、(1)![]() ,
,![]() 都不是对数函数,形如
都不是对数函数,形如![]()
![]() ,且
,且![]() 的函数才是对数函数。
的函数才是对数函数。
(2)①![]() ;
;
②![]() ;
;
③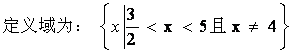 。
。
(3)①求下列函数的值域
1.![]()
②![]()
![]()
③![]()
(4)①![]() 。因为
。因为![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() 。
。
②![]() 。因为
。因为![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() 。
。
③![]() 。
。
![]() 。
。
(5)![]() ;
;![]()
2、(1) ![]() 。因为
。因为![]() ,所以
,所以
![]()
(2) 函数![]() 。
。
因为![]() ,所以函数
,所以函数![]() 。
。
三、题型训练
1、选择题
(1) B
( 如果你选A,说明你掌握了对数函数的图象,但是对于指数函数的图象掌握的不熟练;如果你选C,说明你已经了解了对数函数和指数函数的形状,但是对于底数大于1和底数大于0小于1时的函数图象不熟练;如果你选D,可以看出你掌握了指数函数的图象,只是对于对数函数在底数大于1时的图像掌握的不熟练;因为a>1,函数![]() 与
与![]() 的图象是B。所以正确答案是B)
的图象是B。所以正确答案是B)
(2) A
( 如果你选B,说明你已经掌握了![]() 的解是2,但是对于
的解是2,但是对于![]() 的单调性掌握的不熟练;如果你选C,可以看出你已经掌握了
的单调性掌握的不熟练;如果你选C,可以看出你已经掌握了![]() 的单调性,但是求错了
的单调性,但是求错了![]() 的解;如果你选D,可以看出你已经懂得了对数不等式的解集形式,但是对于函数
的解;如果你选D,可以看出你已经懂得了对数不等式的解集形式,但是对于函数![]() 的单调性和对数方程
的单调性和对数方程![]() 的求解不熟练;因为
的求解不熟练;因为![]() 的解是2,
的解是2,![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]()
![]() 的解集是
的解集是![]() ,正确答案是A)
,正确答案是A)
2、![]()
3、(1)![]() 。
。
因为![]() ,即
,即![]() ,所以
,所以![]() ,
,
所以函数![]()
![]() 。
。
(2)a=3。因为![]() 的反函数的图象过点
的反函数的图象过点![]() ,所以
,所以![]() 的的图象过点
的的图象过点![]() ,所以
,所以![]() ,所以a=3。
,所以a=3。
四、学以致用
1、解:(1)根据对数的运算性质,有![]() ,
,
在![]() 上,随着
上,随着![]() 的增大,
的增大,![]() 减小,相应地
减小,相应地![]() 也减小,即
也减小,即![]() 减小。所以,随着
减小。所以,随着![]() 的增大,
的增大,![]() 减小,即溶液中氢离子的浓度越大,溶液的酸碱度就越大。
减小,即溶液中氢离子的浓度越大,溶液的酸碱度就越大。
(2)当![]() 时,
时,![]() 。所以纯净水的
。所以纯净水的![]() 是7。
是7。
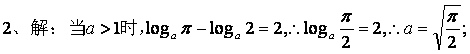

所以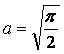 或
或![]() 。
。
| 感动 | 同情 | 无聊 | 愤怒 | 搞笑 | 难过 | 高兴 | 路过 |
- 上一篇:创意法教育学案:对数与对数运算
- 下一篇:创意法教育学案:幂函数
相关文章
-
没有相关内容


 会员登录
会员登录