课题申报实施材料：幂函数

第五课时 幂函数

我的学习目标：

1、通过具体实例了解幂函数的图象和性质；

2、体会幂函数的变化规律及蕴含其中的对称性并能进行简单的应用。

我的学习过程

一、生活引入（5分）

（1）边长为的正方形面积，是的函数；

（2）面积为的正方形边长，是的函数；

（3）边长为的立方体体积，是的函数；

（4）某人内骑车行进了1，则他骑车的平均速度，这里是的函数；

（5）购买每本1元的练习本本，则需支付元，这里是的函数。

以上几个问题中的函数具有什么共同特征？

上述问题中涉及的函数都是形如 _________的函数。

由此引出幂函数的概念。

一般地，形如____________的函数称为幂函数，其中为常数。

二、基本功训练（35分）

1、知识点学习（25分）

（1）知识点1：掌握幂函数的概念（4分）

判断下列函数哪些是幂函数.

①；②；③；④。

形如的函数才是幂函数。

（2）知识点2：熟练常见的5种幂函数的性质（8分）

求解在的单调性。

（3）知识点3：掌握幂函数解析式的求解（5分）

已知幂函数的图象过点，求它的解析式。

（4）知识点4：利用幂函数的图象和性质比较函数值的大小(8分)

比较与的大小

2、知识点演练（共10分，每题5分）

（1）变式演练1：比较与的大小。

（2）变式演练2：讨论的单调性。

三、题型训练

1、选择题(共10分，每题5分)

（1） 若幂函数在上是增函数，则（    ）。

A．>0      B．<0      C．=0        D．=2

（2）函数的图象是（    ）。

           A.       B.      C.      D.

    2、填空题(10分)

（1）与__________________________________

（2）已知幂函数的图象过点，则它的解析式为____

3、解答题(20分)

已知幂函数f（x）＝（p∈Z）在上是增函数，且在其定义域内是偶函数，求p的值，并写出相应的函数f（x）。

四、学以致用

1、 我要解决生活中实际问题。(10分)

在固定压力差（压力差为常数）下，当气体通过圆形管道时，其流量速率R与管道半径r的四次方成正比。

（1）写出函数解析式；

（2）若气体在半径为3cm的管道中，流量速率为400cm³/s，求该气体通过半径为r的管道时，其流量速率R的表达式；

（3）已知（2）中的气体通过的管道半径为5cm，计算该气体的流量速率。

2、每课一测(10分)

讨论函数的定义域、奇偶性、单调性。

附:答案和解析

一、生活引入

；

二、基本功训练

1、（1）①即是幂函数；②、③、④都不是幂函数。形如的函数才是幂函数。

（2）在上是增函数。

（3）。将代入得，所以。

（4）<。因为在上是减函数，所以<。

2、(1) >。因为在是增函数，，所以>。

(2) 在R上是增函数。

三、题型训练

1、选择题

(1) A

（ 如果你选B，说明你认识了幂函数的图象形状，但是对于<0时在上的单调性不熟练；如果你选C，说明你已经了解了幂函数的概念，但是对于=0时在上的单调性掌握的不熟练；如果你选D，可以看出你了解了=2时幂函数在上的单调性，只是对于选择题不能选择这个特殊性的结论，要选择一般性结论；因为>0时，幂函数在上是增函数，所以正确答案是A）

(2) A

（ 如果你选B，说明你已经掌握了在定义域上的单调性，但是对于图象的弯曲形式掌握的不熟练；如果你选C，可以看出你已经了解了幂函数的一种图象，但是没注意到指数是，对于这个特殊幂函数的图象不了解；如果你选D，说明你已经了解了在上的单调性，但是对于在上的单调性不熟练；因为，所以，正确答案是A）

2、（1）

   （2）

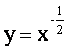
3、；

四、学以致用

1、（1）

（2）

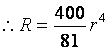
（3）

2、定义域是；是偶函数；在是减函数，在上是增函数。