创意法教育课题学案:余弦定理
人教版数学科高二年级上册
目录
第一章 解三角形
第一节 正弦定理
第二节 余弦定理
....................
第一章 解三角形
第二节 余弦定理
第一课时
●教学目标
知识与技能:掌握余弦定理的两种表示形式及证明余弦定理的向量方法,并会运 用余弦定理解决两类基本的解三角形问题。
过程与方法:利用向量的数量积推出余弦定理及其推论,并通过实践演算掌握运用余弦定理解决两类基本的解三角形问题
情感态度与价值观:培养学生在方程思想的指导下处理解三角形问题的运算能力。
我的学习过程
一、生活引入
1.每课一诵(5分)
正弦定理:
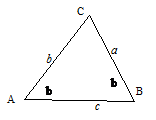 2. 修建一条高速公路,要开凿隧道将一段山体打通.现要测量该山体底侧两点间的距离,即要测量该山体两底侧A、B两点间的距离(如图1).请想办法解决这个问题. (5分)
2. 修建一条高速公路,要开凿隧道将一段山体打通.现要测量该山体底侧两点间的距离,即要测量该山体两底侧A、B两点间的距离(如图1).请想办法解决这个问题. (5分)
这是一个学生身边的实际应用问题,在其解决的
过程中得到余弦定理,引出课题。
二、基本功训练
1.知识点学习
(1)知识点1: 余弦定理的证明
联系已经学过的知识和方法,可用什么途径来解决这个问题?
用正弦定理试求,发现因A、B均未知,所以较难求边c。
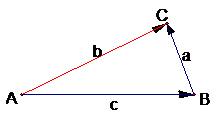 由于涉及边长问题,从而可以考虑用向量来研究这个问题。 A如图1.1-5,设
由于涉及边长问题,从而可以考虑用向量来研究这个问题。 A如图1.1-5,设![]() ,
,![]() ,
,![]() ,那么
,那么![]() ,则
,则 ![]()
![]()
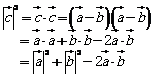
从而 ![]() (图1.1-5)
(图1.1-5)
同理可证 ![]()
![]()
于是得到以下定理
余弦定理:三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍。即
![]()
![]()
![]() ...........(10分)
...........(10分)
简易分析:此题实际上属于( )问题
(2)知识点2:(10分)
简易分析:余弦定理的变形
![]()
![]()
![]()
(3)知识点3:定理的理解 (10分)
①已知三角形的任意两边及它们的夹角就可以求出第三边;
②已知三角形的三条边就可以求出其它角。
2.知识点演练
例1在![]() 中,已知
中,已知![]() ,解此三角形。
,解此三角形。
变式演练1:在![]() 中,已知
中,已知![]() ,
, ![]() ,
, ![]() .求
.求![]() 和
和![]() .
.
变式演练2 已知![]() 中,
中,![]() 、
、![]() 、
、![]() ,求
,求![]() 中的最大角
中的最大角
例2. 在![]() 中,已知角
中,已知角![]() 所对的三边长分别为
所对的三边长分别为![]() ,若
,若![]() ,
,![]() ,
,![]() ,求角
,求角![]() 和
和![]()
变式演练1:在![]() 中,角
中,角![]() 所对的三边长分别为
所对的三边长分别为![]() ,若
,若![]()
![]() ,求
,求![]() 的各角的大小.(10分)
的各角的大小.(10分)
变式演练2.在![]() 中,若
中,若![]() ,求角
,求角![]() .
.
三、题型训练
1.选择题( )
(1)在△ABC中,bCosA=acosB,则三角形为( )
A直角三角形 B锐角三角形C等腰三角形D等边三角形
(2)已知a,b,c是△ABC三边之长,若满足等式(a+b-c)(a+b+c)=ab,
则角C的大小为 ( )
A.60° B.90° C.120° D.150°
(3)若△ABC的三个内角满足sin A∶sin B∶sin C=5∶11∶13,则△ABC( )
A.一定是锐角三角形
B.一定是直角三角形
C.一定是钝角三角形
D.可能是锐角三角形,也可能是钝角三角形
2填空题
(1)在△ABC中,若a2>b2+c2,则△ABC为_________________;若a2=b2+c2,则△ABC为 ;若a2<b2+c2且b2<a2+c2且c2<a2+b2,则△ABC为
(2)已知△ABC三边满足a2+b2=c2-ab,则此三角形的最大内角为________.
3.解答题
在△ABC中,若(a+b+c)(b+c-a)=bc,并且sinA=2sinBcosC,试判断△ABC的形状.
参考答案
每课一诵:![]()
1.已知两角及其一边可以求其他边。
2.已知两边及其一边的对角
例1 解:由余弦定理:![]()
![]()
![]() ,
,![]() ;
;
![]() ;
;
变式演练1 【答案】由余弦定理得:![]() ,
,
∴![]()
由正弦定理得:![]()
因为![]() 为钝角,则
为钝角,则![]() 为锐角, ∴
为锐角, ∴![]() .
.
∴![]()
变式演练2∵三边中![]() 最大,∴
最大,∴![]() 其所对角
其所对角![]() 最大,
最大,
根据余弦定理:![]() ,
,
∵ ![]() , ∴
, ∴![]()
故![]() 中的最大角是
中的最大角是![]() .
.
例2.【答案】根据余弦定理可得:

∵![]() , ∴
, ∴ ![]() ;
;
∴由正弦定理得: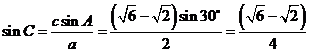 .
.
变式演练1:
设![]() ,
,![]() ,
,![]() ,
,![]()
根据余弦定理得: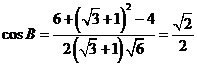 ,
,
∵![]() ,∴
,∴![]() ;
;
同理可得![]() ;
;
∴![]()
变式演练2【答案】∵![]() , ∴
, ∴![]()
∵![]() , ∴
, ∴![]()
。
三、题型训练
1.选择题(1)C (2)C (3)C
(2)解析:由(a+b-c)(a+b+c)=ab得(a+b)2-c2=ab.c2=a2+b2+ab=a2+b2-2abcos C.
∴cos C=-,C=120°.
(3)解析:∵sin A∶sin B∶sin C=a∶b∶c
∴a∶b∶c=5∶11∶13
设a=5k,b=11k,c=13k,
则cos C===-<0,
∴C为钝角.
2.填空题
(1)钝角三角形,直角三角形,锐角三角形
(2)解析:∵a2+b2-c2=-ab,
∴cos C==-,
故C=150°为三角形的最大内角.
答案:150°
3.解答题.
解:由已知条件(a+b+c)(b+c-a)=bc及余弦定理得
cosA===
∴A=60°
又由已知条件sinA=2sinBcosC得sin(B+C)=sin(B+C)+sin(B-C)
∴sin(C-B)=0,∴B=C
于是有A=B=C=60°,
故△ABC为等边三角形.
| 感动 | 同情 | 无聊 | 愤怒 | 搞笑 | 难过 | 高兴 | 路过 |
相关文章
-
没有相关内容


 会员登录
会员登录